Metamorphic Truth
Posted by Haw-minn Lu in Machine Learning
What is Metamorphic Truth?
Metamorphic truth is a method of training an Artificial Neural Network (ANN) where the "truth" supplied during training is not fixed and may depend on the prediction made by the ANN. More specifically during training a truth metamorphism is defined as a function of the prediction, the ground truth, and perhaps additional metadata.
History and Concept
The concept arose when building a denoising autoencoder with missing data. The obvious approach of filling in the missing data with dummy data may work well but could also ultimately distort the loss function. By viewing ANN training as a feedback system, it became clear that the loss function should somehow ignore the dummy filled-in data and thus remove the downstream bias from these terms. Then, the mean square error (MSE) error would look like
where \(S_{\mathrm{notmissing}}\) is the set of indexes for which \(y_i\) is not missing and \({\tilde{\mathbf{y}}}\) is the predicted value.
From the perspective of a feedback system, any prediction the autoencoder makes is acceptable, or, in lay terms, "your guess is as good as mine." Detailed discussion of this type of autoencoder can be found in our paper.
Unfortunately, there are several practical problems. In our missing data problem, the attributes \(\{y_i\}\) that are missing may change based on the present sample so the loss function would be specific to which sample is being used to train the autoencoder. Most machine learning packages do not allow sample by sample customization of the loss function.
As a practical consideration, rather than dismantling the structure of established machine learning libraries or contriving a complex loss function, it was much simpler to alter the so-called "ground truth" that is fed back into the autoencoder during learning using a standard MSE loss function:
where \(N\) is the dimension of the output vector and \(\bar y_i\) is given by the following:
This mapping cancels the dummy \(y_i\) values in the loss function, thus removing its effects. This mapping is defined as a truth metamorphism.
Learning Implications
What started out as a "hack" for implementing a desired mathematical calculation has much broader implications to learning. From one perspective, rigid ground truths can be thought of as another form of overtraining. In practice, there may be ambiguous labels and by enforcing a fixed ground truth for each output in training, you may be preventing the network from exploring other potential minima consistent with the label-ambiguity.
For example, human learning with feedback tailored to an individual's current understanding usually works better. Learning from a books is like the rigid ground truth model, whereas learning from a live teacher is like the metamorphic truth model. When learning from the book, the "truth" doesn't change no matter how many times you read it, though your understanding might improved each time. When learning from a live teacher, one might get an indication that the answer is close enough to the answer the teacher originally wanted.
Formalizing the Concept
Despite the variety of architectures, ANNs that implement the multilayer perceptron have a common output layer that computes the following:
where \(w_{i,j}\) are the weights from the output layer, \(x_{j}\) are the outputs from the last hidden layer and \(L_\mathrm{output}\) is the number of units in the output layer. For the mean square error, the loss function is defined as:
Typical gradient descent algorithms start by calculating the derivative of the error with respect to the weights and apply it first to the output layer and then the the hidden layers via the chain-rule,
Using the MSE this becomes
To train using metamorphic truth, we define a truth metamorphism: \(\bar{\mathbf{y}}=\cal{M}(\mathbf{y}, \mathbf{\tilde {y}})\) and we define the loss function of \(\mathbf{\bar y}\) as opposed to the ground truth \(\mathbf{y}\). Treating the metamorphism as a function just gives a more complex loss function. What separates a metamorphism from simply another loss function is that we define the following,
where we have extrapolated \({\partial \bar{y_i}}/{\partial w_{j,i}} = 0\) from \({\partial {y_i}}/{\partial w_{j,i}} = 0\). In non-mathematical terms, the truth metamorph is treated exactly like the ground truth. The result is that all the learning algorithms can proceed unchanged once the truth metamorph is substituted for the ground truth.
Potential Mathematical Implications
No doubt a lot of question arises by this "hacking" of the mathematics. In essence, what has been done is the error surface for which a gradient descent algorithm changes during the learning process making it possibly a moving target for the ANN model which may result in oscillations that make the minima harder to find. Practically speaking, it is too early to tell if this is a potential problem. However, should it proved to be a problem, a lesson from feedback systems can be applied. Whenever a system is in danger of instability, a dampening agent of some sort is imposed. In fact, in modern stocastic gradient descent elements of dampening are introduced already (e.g., batch-learning, momentum). Our one practical application of metamorphic truth for data imputation does not suffer these issues.
Examples of Situations to Use Metamorphic Truth
The following are some examples of where metamorphic truth might be applicable. We have not had detailed case study on any of these except the "Don't Care" example which has been incorporated into an autoencoder for imputation as mentioned above.
Don't Care
In some models there are cases where the output is irrelevant. For example, certain states in logic design are ignored (see here). The imputation example is a situation where the predicted value from a missing data element is irrelevant.
As another example, consider a model that predicts medical conditions and gender. If the output is a gender-specific condition (such as pregnancy), one might choose to ignore the corresponding gender output as a postprocessing step Hence, in these cases you don't care what the prediction is and metamorphic truth allows you to train a model in this way if desired.
In this example, the metamorphism is similar to the one given above:
Multiple Answers
Consider the following digits from the MNIST database:
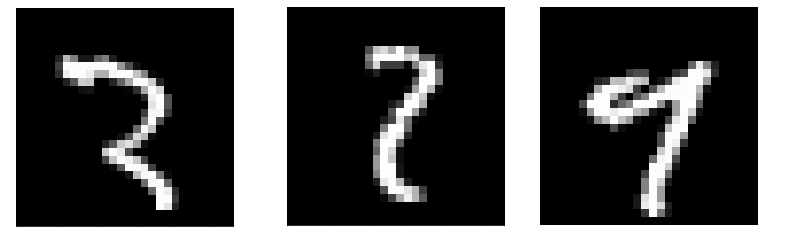
These are three ambiguous numerals. Without disclosing the truth value in the
MNIST database, one could probably make the case that the first number is a 2
or an incomplete 3. The second number could be a 2 or a 7 and the third a
7 and a 9.
Suppose the middle number was labelled as a 7 one could make the case that
this was labelled incorrectly or the person labelling the samples was taught to
write numbers a little differently so that what seems like it should be a 2
in your eyes could be a 7 in the labeller's eyes. Perhaps the entire dataset
is labeled by multiple people. There could be a lack of
consistency in the way the numbers are labeled. Even if the person who labeled
the digit is the actual person who wrote it, it may very well be that the way
they wrote the number 7 is outside the norm of how the digit is drawn.
For all of the above reasons, it is possible that these cases could adversely
bias an ANN's learning. For this reason, one might want to say that both 2
and 3 are acceptable answers to the first classification and 2 and 7 are
acceptible answers to the second classification etc.
One can implement this kind of training by putting multiple values for each \(\bf y\). The metamorphism takes the predicted values and returns the closest correct answer to the prediction.
Confidence Labels
In some situations, there may be a small subset of impeccably labeled data and a larger set of less reliable data that you want to incorporate into learning. You could define a metamorphism
where \(\alpha\) is a confidence value in the truth for that particular sample and attribute. This metamorphism gives more or less weight to a truth value based on the confidence and inversely weights the contribution of the prediciton
Implementational Issues
While originally developed for a multiple imputation autoencoder using
tensorflow, it is unclear how to implement metamorphic truth with other
popular machine learning packages. The following is a high level description
of how to implement it in tensorflow. The metamorphism function takes the
predicted output, the ground truth output, and a sample index as input. The
sample index is used to access metadata when necessary. For example in the
imputation problem the attributes that are missing vary from sample to sample,
so the index keeps track of which sample is transformed by the
metamorphism.
The basic idea is to append the index of the training sample to the training output to retain the order if the samples are scrambled. This index is then stripped off in the loss function when the metamorphism is applied.
When you compile a Tensorflow model, you specify a customized loss function.
The loss function will first split the index from the truth value (recall we
appended the index to it), leaving the truth value without the index. The truth
value, predicted value and index are fed into the metamorphism.
For tensorflow you must turn the output of the metamorphism into a constant
with respect to the model as tensorflow will build a computation graph and
try to compute the gradient of the metamorphism (which may have complicated
discontinuities). To compensate for this, we construct a custom function
zero_derivative, as follows
@tf.custom_gradient
def zero_derivative(x):
def grad(dy):
return tf.zeros_like(dy)
return x, grad
This 'function' is the identity function with a zero derivative. In effect, it
turns the operand x into a constant. Finally, when you run fit you supply
as the training output, the original training output with the index appended to
each sample.
Conclusion
Metamorphic truth expands the use cases for deep learning networks to situations with ambiguous labeling or in situations with outputs that are irrelevant. Real applications for metamorphic truth are limited to date and the theoretical and practical implementation study metamorphic truth is just beginning.